Hierarchical computation with Langroid Agents¶

Here is a simple example showing tree-structured computation where each node in the tree is handled by a separate agent. This is a toy numerical example, and illustrates:

how to have agents organized in a hierarchical structure to accomplish a task
the use of global state accessible to all agents, and
the use of tools/function-calling.

The Computation¶

We want to carry out the following calculation for a given input number \(n\):

def Main(n):
    if n is odd:
        return (3*n+1) + n
    else:
        if n is divisible by 10:
            return n/10 + n
        else:
            return n/2 + n

Using function composition¶

Imagine we want to do this calculation using a few auxiliary functions:

def Main(n):
    # return non-null value computed by Odd or Even
    Record n as global variable # to be used by Adder below
    return Odd(n) or Even(n)

def Odd(n):
    # Handle odd n
    if n is odd:
        new = 3*n+1
        return Adder(new)
    else:
        return None

def Even(n):
    # Handle even n: return non-null value computed by EvenZ or EvenNZ
    return EvenZ(n) or EvenNZ(n)

def EvenZ(n):
    # Handle even n divisible by 10, i.e. ending in Zero
    if n is divisible by 10:
        new = n/10
        return Adder(new)
    else:
        return None

def EvenNZ(n):
    # Handle even n not divisible by 10, i.e. not ending in Zero
    if n is not divisible by 10:
        new = n/2
        return Adder(new)
    else:
        return None  

def Adder(new):
    # Add new to starting number, available as global variable n
    return new + n

Mapping to a tree structure¶

This compositional/nested computation can be represented as a tree:

       Main
     /     \
  Even     Odd
  /   \        \
EvenZ  EvenNZ   Adder
  |      |
 Adder  Adder

Let us specify the behavior we would like for each node, in a "decoupled" way, i.e. we don't want a node to be aware of the other nodes. As we see later, this decoupled design maps very well onto Langroid's multi-agent task orchestration. To completely define the node behavior, we need to specify how it handles an "incoming" number \(n\) (from a parent node or user), and how it handles a "result" number \(r\) (from a child node).

Main:
- incoming \(n\): simply send down \(n\), record the starting number \(n_0 = n\) as a global variable.
- result \(r\): return \(r\).
Odd:
- incoming \(n\): if n is odd, send down \(3*n+1\), else return None
- result \(r\): return \(r\)
Even:
- incoming \(n\): if n is even, send down \(n\), else return None
- result \(r\): return \(r\)
EvenZ: (guaranteed by the tree hierarchy, to receive an even number.)
- incoming \(n\): if n is divisible by 10, send down \(n/10\), else return None
- result \(r\): return \(r\)
EvenNZ: (guaranteed by the tree hierarchy, to receive an even number.)
- incoming \(n\): if n is not divisible by 10, send down \(n/2\), else return None
- result \(r\): return \(r\)
Adder:
- incoming \(n\): return \(n + n_0\) where \(n_0\) is the starting number recorded by Main as a global variable.
- result \(r\): Not applicable since Adder is a leaf node.

From tree nodes to Langroid Agents¶

Let us see how we can perform this calculation using multiple Langroid agents, where

we define an agent corresponding to each of the nodes above, namely Main, Odd, Even, EvenZ, EvenNZ, and Adder.
we wrap each Agent into a Task, and use the Task.add_subtask() method to connect the agents into the desired hierarchical structure.

Below is one way to do this using Langroid. We designed this with the following desirable features:

Decoupling: Each agent is instructed separately, without mention of any other agents (E.g. Even agent does not know about Odd Agent, EvenZ agent, etc). In particular, this means agents will not be "addressing" their message to specific other agents, e.g. send number to Odd agent when number is odd, etc. Allowing addressing would make the solution easier to implement, but would not be a decoupled solution. Instead, we want Agents to simply put the number "out there", and have it handled by an applicable agent, in the task loop (which consists of the agent's responders, plus any sub-task run methods).
Simplicity: Keep the agent instructions relatively simple. We would not want a solution where we have to instruct the agents (their LLMs) in convoluted ways.

One way naive solutions fail is because agents are not able to distinguish between a number that is being "sent down" the tree as input, and a number that is being "sent up" the tree as a result from a child node.

We use a simple trick: we instruct the LLM to mark returned values using the RESULT keyword, and instruct the LLMs on how to handle numbers that come with RESULT keyword, and those that don't In addition, we leverage some features of Langroid's task orchestration:

When llm_delegate is True, if the LLM says DONE [rest of msg], the task is considered done, and the result of the task is [rest of msg] (i.e the part after DONE).
In the task loop's step() function (which seeks a valid message during a turn of the conversation) when any responder says DO-NOT-KNOW, it is not considered a valid message, and the search continues to other responders, in round-robin fashion.

See the chat-tree.py example for an implementation of this solution. You can run that example as follows:

python3 examples/basic/chat-tree.py

In the sections below we explain the code in more detail.

Define the agents¶

Let us start with defining the configuration to be used by all agents:

from langroid.agent.chat_agent import ChatAgent, ChatAgentConfig
from langroid.language_models.openai_gpt import OpenAIChatModel, OpenAIGPTConfig

config = ChatAgentConfig(
  llm=OpenAIGPTConfig(
    chat_model=OpenAIChatModel.GPT4,
  ),
  vecdb=None, # no need for a vector database
)

Next we define each of the agents, for example:

main_agent = ChatAgent(config)

and similarly for the other agents.

Wrap each Agent in a Task¶

To allow agent interactions, the first step is to wrap each agent in a Task. When we define the task, we pass in the instructions above as part of the system message. Recall the instructions for the Main agent:

Main:
- incoming \(n\): simply send down \(n\), record the starting number \(n_0 = n\) as a global variable.
- result \(r\): return \(r\).

We include the equivalent of these instructions in the main_task that wraps the main_agent:

from langroid.agent.task import Task

main_task = Task(
    main_agent,
    name="Main",
    interactive=False, #(1)!
    system_message="""
          You will receive two types of messages, to which you will respond as follows:

          INPUT Message format: <number>
          In this case simply write the <number>, say nothing else.

          RESULT Message format: RESULT <number>
          In this case simply say "DONE <number>", e.g.:
          DONE 19

          To start off, ask the user for the initial number, 
          using the `ask_num` tool/function.
          """,
    llm_delegate=True, # allow LLM to control end of task via DONE
    single_round=False,
)

Non-interactive: don't wait for user input in each turn

There are a couple of points to highlight about the system_message value in this task definition:

When the Main agent receives just a number, it simply writes out that number, and in the Langroid Task loop, this number becomes the "current pending message" to be handled by one of the sub-tasks, i.e. Even, Odd. Note that these sub-tasks are not mentioned in the system message, consistent with the decoupling principle.
As soon as either of these sub-tasks returns a non-Null response, in the format "RESULT ", the Main agent is instructed to return this result saying "DONE ". Since llm_delegate is set to True (meaning the LLM can decide when the task has ended), this causes the Main task to be considered finished and the task loop is exited.

Since we want the Main agent to record the initial number as a global variable, we use a tool/function AskNum defined as follows (see this section in the getting started guide for more details on Tools):

from rich.prompt import Prompt
from langroid.agent.tool_message import ToolMessage


class AskNumTool(ToolMessage):
  request = "ask_num"
  purpose = "Ask user for the initial number"

  def handle(self) -> str:
    """
    This is a stateless tool (i.e. does not use any Agent member vars), so we can
    define the handler right here, instead of defining an `ask_num`
    method in the agent.
    """
    num = Prompt.ask("Enter a number")
    # record this in global state, so other agents can access it
    MyGlobalState.set_values(number=num)
    return str(num)

We then enable the main_agent to use and handle messages that conform to the AskNum tool spec:

main_agent.enable_message(AskNumTool)

Using and Handling a tool/function

"Using" a tool means the agent's LLM generates the function-call (if using OpenAI function-calling) or the JSON structure (if using Langroid's native tools mechanism) corresponding to this tool. "Handling" a tool refers to the Agent's method recognizing the tool and executing the corresponding code.

The tasks for other agents are defined similarly. We will only note here that the Adder agent needs a special tool AddNumTool to be able to add the current number to the initial number set by the Main agent.

Connect the tasks into a tree structure¶

So far, we have wrapped each agent in a task, in isolation, and there is no connection between the tasks. The final step is to connect the tasks to the tree structure we saw earlier:

main_task.add_sub_task([even_task, odd_task])
even_task.add_sub_task([evenz_task, even_nz_task])
evenz_task.add_sub_task(adder_task)
even_nz_task.add_sub_task(adder_task)
odd_task.add_sub_task(adder_task)

Now all that remains is to run the main task:

main_task.run()

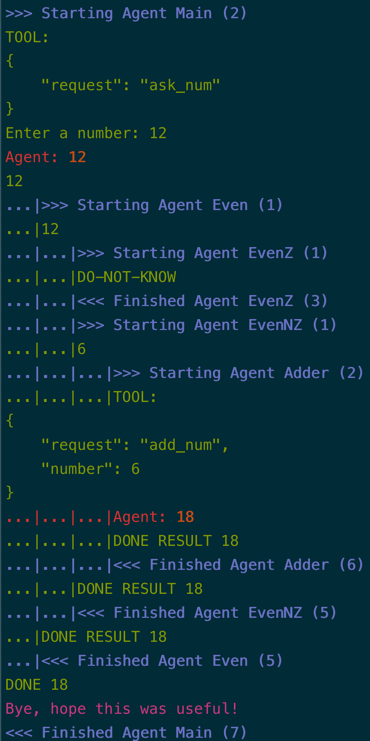
Here is what a run starting with \(n=12\) looks like: